- Details
- Veröffentlicht: 28. November 2017
Beitragsseiten
Zunächst werden wir uns deskriptive, also nur beschreibende Statistiken ansehen. Dies ist grundsätzlich vor weiteren Analysen zu empfehlen, um ein Gefühl für die Daten und die Verteilung der zentralen Variablen zu erhalten. Zunächst legen wir unsere Kontrollvariablen fest, um unsere Stichprobe auswählen zu können. Um die Analyse einfach zu halten, werden wir nur für Alter, Bildungslevel und Einkommen kontrollieren, da wir annehmen, dass diese Faktoren signifikant auf die Attraktivität einer Person einwirken. Bildung könnte beispielsweise deshalb wichtig sein, weil höher gebildete Personen einen anderen Geschmack (in Bezug auf Kleidungsstil, Einrichtung, etc...) aufweisen, was die Attraktivität beeinflussen könnte. Das Geschlecht kontrollieren wir implizit durch das Design der Analysen. Wir entfernen alle Personen, die einen oder mehrere fehlende Werte auf eine dieser Variablen aufweisen, aus dem Sample. Am Ende bleiben 2694 Fälle übrig.
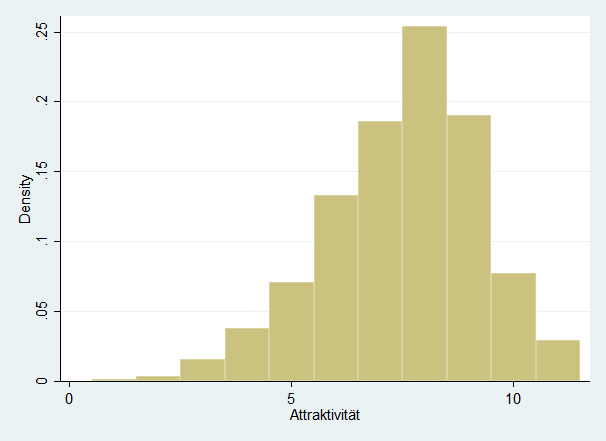
Beginnen wir damit, uns die Verteilung der Attraktivitätsvariable (abhängige Variable) anzusehen. Dazu ist ein Histogram geeignet. Wie wir sehen, nähert sich diese Verteilung grob einer Normalverteilung an. Der Modus ist Kategorie 8, also ein relativ hoher Wert. Offensichtlich ist die Attraktivität der Gesamtbevölkerung relativ hoch. Auch zeigt die Verteilung, dass die meisten der Kategorien ausreichend besetzt sind. Wir können daher die Variable daher als metrisch betrachten, was die Analysen erleichtert. Streng genommen ist die Variable ordinalskaliert, was wir zumindest anmerken sollten.
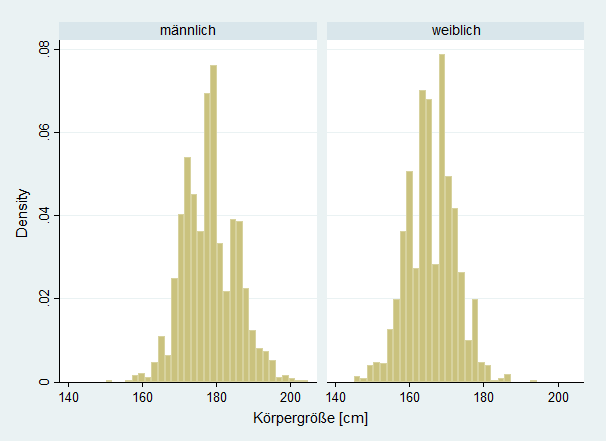
Die zweite zentrale Variable ist die Körpergröße. Da diese in Zentimetern gemessen wird, liegt eine klar metrische Variable vor. Hier trennen wir die Darstellung nach Geschlecht, da wir erhebliche Differenzen erwarten. Tatsächlich erkennt man die Unterschiede klar, die allgemeine Normalverteilungsannährung jedoch auch. Männer sind im Schnitt größer als Frauen. Die Verteilung der übrigen Variablen ist weniger aufregend. Jedoch werden die Variablen zur Verbesserung der Analyse transformiert. Der höchste Schulabschluss wurde in drei Kategorien rekodiert (Hauptschulabschluss oder kein Abschluss, Mittlere Reife, Abitur oder Fachabitur). Das Einkommen ist wie üblich sehr ungleich verteilt, sodass dieses durch den Logarithmus transfomiert wird. Danach nähert sich auch dieses einer Normalverteilung an.
Eine weitere Anmerkung: streng genommen müssten alle Ergebnisse gewichtet werden, da Personen aus Ostdeutschland im ALLBUS planmäßig überrepräsentiert sind. Dies ist immer dann wichtig, wenn wir erwarten würden, dass signifikante Unterschiede zwischen West und Ost bestehen. Problematisch ist, dass unser Multilevelmodell keine Gewichtung erlaubt. Grund ist schlichtweg, dass die Statistiker (noch) nicht wirklich wissen, wie man Multilevelmodelle und Gewichte miteinander kombiniert und richtige Ergebnisse erhält. Deshalb sind grundsätzlich alle Statistiken in dieser Analyse nicht gewichtet, was Verzerrungen verursachen könnte. Ein einfacher t-Test zeigt beispielsweise, dass sich die Körpergröße in West und Ost signifikant unterscheiden: Personen in Westdeutschland sind im Schnitt 1,19 cm größer als Personen aus dem Osten (p = 0,001, n = 2694). In diesem Falle müsste man abwägen, ob einem die Gewichtung oder die Multilevel-Modellierung wichtiger ist. Wir entscheiden uns hier für das Multilevel.

