- Details
- Veröffentlicht: 28. November 2017
Beitragsseiten
Kommen wir nun zu den eigentlichen Analysen. Wie bereits beschrieben werden wir vier verschiedene Modelle berechnen, um den Einfluss des Geschlechts angeben zu können. Wir betreiben der Einfachheit halber keinen schrittweisen Modellaufbau, sondern nehmen direkt alle Variablen mit in das Modell. Eine Alternative ist es, zuerst als einzigen Prädiktor die Körpergröße aufzunehmen und anschließend die Kontrollvariablen hinzuzufügen. Um zu testen, ob sich die Modelle unterscheiden, kann anschließend ein Likelihood-Ratio-Test verwendet werden. Im Do-File findet sich ein Beispiel, wie dies angewendet werden kann. Zunächst fassen wir die Ergebnisse knapp in einer einfachen Tabelle zusammen:
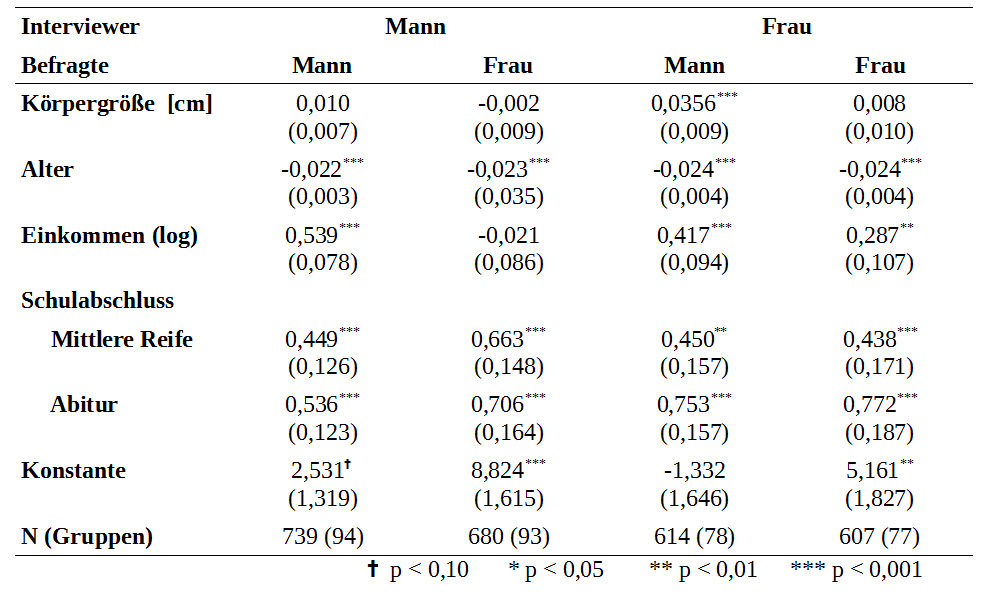
Die Interpretation ist wie folgt: positive, signifikante Koeffizienten bedeuten, dass höhere Werte mit höherer Attraktivität einhergehen. Die nominalskalierte Variable Schulabschluss hat als Referenz "Hauptschulabschluss oder kein Abschluss". Insgesamt wird deutlich, dass die Körpergröße nur dann eine Rolle spielt, wenn Frauen Männer interviewen: jeder Zentimeter mehr an Körpergröße erhöht dann die Attraktivität um 0,036 Punkte (unter Konstanthaltung aller anderen Variablen). Der Effekt ist hochsignifikant. Das Fazit lautet also: in den Augen von Frauen ist die Körpergröße bei Männern ein Faktor, der auf die Attraktivität einwirkt und größere Männer sind im Schnitt attraktiver. Die Interpretation der anderen Variablen kann zum Üben von Effekten genutzt werden. Noch ein Beispiel für den Schulabschluss (Männer interviewen Frauen): Personen mit Abitur sind im Vergleich zu Personen mit Hauptschulabschluss im Schnitt 0,71Punkte attraktiver. Bildung macht also doch sexy...
Zur Übung ist die Originalausgabe von Stata für das dritte Modell (Frauen interviewen Männer) angegeben. Hierbei sollen noch kurz einige Dinge angemerkt werden:
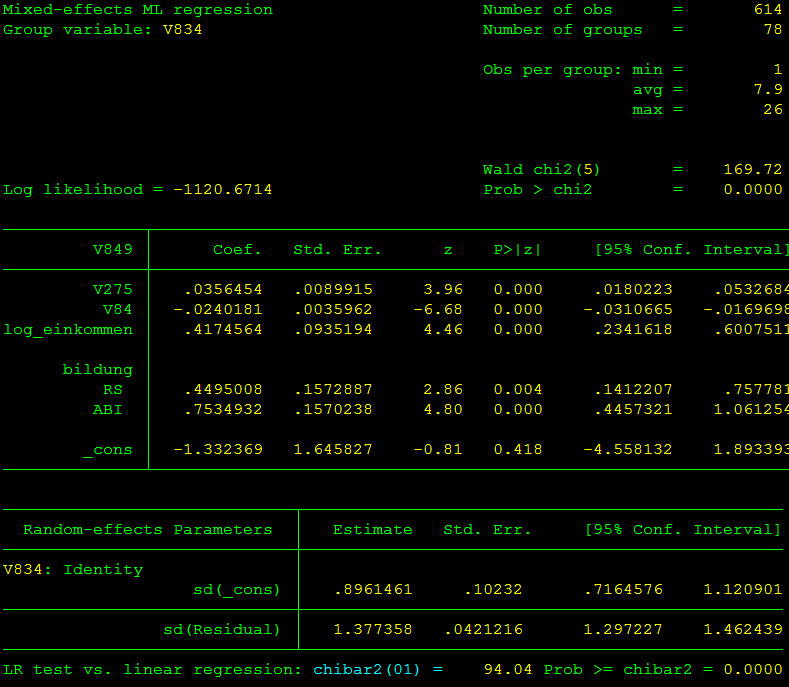
Oben rechts sehen wir zunächst N (614) und die Anzahl der Gruppen (78), also die Anzahl der Interviewer. Im Schnitt hat ein Interviewer 7,9 Personen interviewt. Unten sehen wir die Informationen zur Nestingvariable Interviewer (V834). Der LR test (letzte Zeile) ist hochsignifikant (0.0000) was uns zeigt, dass es signifikante Unterschiede zwischen den Interviewern gibt. Die Anwendung eines Multilevelmodels ist daher absolut gerechtfertigt. Die Intraklassenkorrelation ergibt sich aus (0,896^2) / (0,896^2 + 1,377^2) = 0,297 (oder über den Befehl estat icc). Dies bedeutet, dass es durchaus Gemeinsamkeiten innerhalb der Gruppen gibt. Ein Wert von 1 würde bedeuten, dass alle Befragten innerhalb einer Gruppe identisch wären.
Zum Abschluss eine kurze Diagnostik. Bei Regressionen teste man normalerweise, ob die Residuen normalverteilt sind. Ist dieses Kriterium nicht erfüllt, kann es sein, dass wichtige Variablen im Modell fehlen. Erkennt man beispielsweise Muster im Plot der Residuen, so kann es sein, dass ein Interaktionsterm fehlt. Um dies zu testen führen wir (hier im Beispiel nach Modell 3) folgende Befehle aus (siehe Do-File) und erhalten diese Ausgabe:
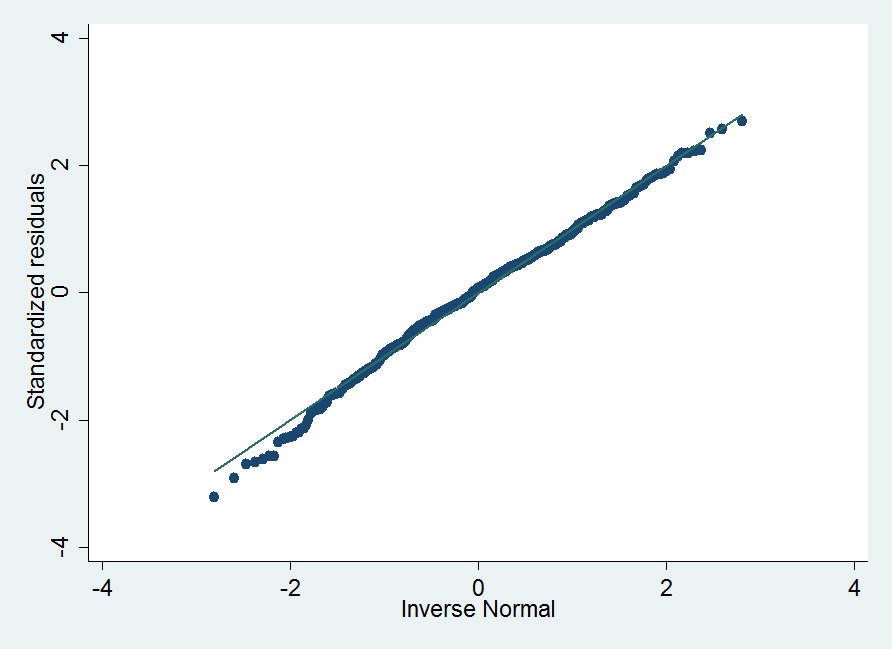
Wie wir feststellen, liegen die Residuen fast perfekt auf einer Geraden, was die approximative Normalverteilung beweist. Dies ist grundsätzlich ein positives Kriterium, was unsere Inferenz absichert.

